Graphs of Tangent, Cotangent, Cosecant, and Secant functions

Graph of the Tangent Function

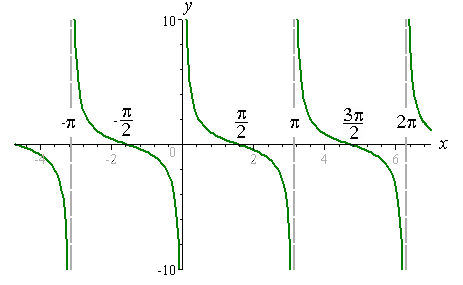
The tangent function is odd, therefore the graph y=tanx is symmetric with respect to the origin. 

tan(θ) =sin(θ)/cos(θ)

tangent is then undefined when cosx=0. When there is a zero in the denominator, you put a vertical asymptote there.

The vertical asymptotes will be at –π/2, π/2, and3π/2

Tangent will be zero when the numerator Sinx=0. The x intercepts will then be at 0, π, 2π, - π, -2π

The period for tangent functions is  therefore for y=tanx, the period is  π

Graph of the Cotangent Function

Lets start with y=cotx=Cosx/Sinx

Because Sinx=0 would make the function undefined, values that make it Sinx=0 will be the Vertical Asymptotes.

The vertical asymptotes are at -2π, -π, π, 2π

Because Cosx=0 would make Cotangent 0, values that make Cosx=0 will be the X-Intercepts

The x-intercepts will be –π/2, π/2, and3π/2

y=cotx, the period is  π

Graphs of Secant functions

secx=1/cosx

The asymptotes of secx will be the same of tanx, which are -, , 3π/2, -3π/2

It is important to draw out the reciprocal function and take the reciprocals of the y-coordinate to obtain points for the graph.

The period would be still 2

Because secx is even, it will be centered around the origin.

Graphs of Cosecant functions

cscx=1/sinx

The asymptotes of cscx will be the smae of cotx which are –π/2, π/2, and3π/2

It is important to draw out the reciprocal function and take the reciprocals of the y-coordinate to obtain points for the graph.

Period is still 2π

Because cscx is odd, the graph will be centered around the origin.