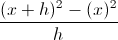One-to-One Functions

According to our textbook, a function f is one-to-one if, for a and b in its domain,  f(a) = f(b)  implies that  a = b. 

To have an inverse, a function must be one-to-one. This means that no two elements in the domain of f correspond to the same element in the range of f. 


Testing for One-to-One Functions

Ex. Is g(x) = 3x - 2  one-to-one?

   See if g(a) = g(b) implies that a = b

   Substitute a for x and b for x. 

     6a - 2 = 6b - 2  (add 2 to both sides)

     6a = 6b   (Divide by 6)

       a = b

This is a one-to-one function!


Ex.  Is the function f(x) =   one-to-one?   

       (Multiply numerator by 5)

  (Simplify) 

   3a + 4 = 3b + 4   (Subtract 4 from both sides)


      3a = 3b     (Divide by 3)

     a = b

This is a one-to-one function!

Ex.  Is the function f(x) =  one-to-one?

     Let a and b be nonnegative real numbers with f(a) = f(b).

    

         (Subtract 1 from both sides)

        (Square both sides)

         a = b

Therefore,  f(a) = f(b), implies that a = b.   So,  f is one-to-one. 

Look at it this way:

 (0, 1)   (5, 2)   (6, 4)

Domain:  0, 5, 6

Range:  1, 2, 4

Each element in the domain (0, 5, and 6) correspond with a unique element in the range (1, 2, and 4)

Sometimes, always, never...

 An odd function is one-to-one... SOMETIMES

An even function is one-to-one... NEVER

Links to look at:

http://www.mathwarehouse.com/algebra/relation/one-to-one-function.php

http://www.mathwords.com/o/one_to_one_function.htm

Compositions of functions

A composition of a function is another way to combine two functions. A composition of a function is usually seen as or .
You read as F of G of X and as G of F of X.
= f(g(x)) and =g(f(x)).
To solve a composition of functions you simply plug g(x) into f(x) and solve.

Here is an example with an explanation:
Solve , where f(x)=x² + 3x and g(x)=x+12
You know that =f(g(x)) so you plug g(x) into f(g(x)) and get f(x+12).
You then solve the equation f(x) =x² + 3x but instead of f(x) you want to use f(g(x)) which we found to be f(x+12).
f(x+12)=(x+12)² +3(x+12) Simply the composition to get a solution
            =x²+24x+144+3x+36
            = x²+27x+180

This works for any set of values for f(x) and g(x), however and do not always produce the same products. In this case f(x) or g(x) will either be a square root or a radical.
For some more information and help check out:
http://www.purplemath.com/modules/fcncomp3.htm
http://www.youtube.com/watch?v=1x7gv3N6FD8

Brandon McCann

Inverse Functions

All inverse functions have to be the inverse of a one-to-one functions.

A one-to-one function is a function with an output (range/ y-value) with one input (domain/ x-value).

The function above is one-to-one because the horizontal line goes through the function once.

The function above is NOT one-to-one because the horizontal line goes through the function twice.

The function above is one-to-one because the horizontal line goes through the function once.

Please note that quadratic equations are never one-to-one functions because the horizontal crosses through the function twice.

Always know that one-to-one functions always have an inverse that is a function. For example, the inverse of a quadratic is not a function because the vertical line would cross through it twice.

Please note that even functions can never be one-to-one because they one-to-one functions can never have an output with a positive and negative input. The horizontal line would have to cross the function more than once if the function is symmetrical across the y-axis.

PLEASE NOTE THIS IN THE GRAPH BELOW

Sometimes, odd functions can be one-to-one because one-to-one functions can sometimes have a positive input with positive output and a negative input with a negative output.

PLEASE NOTE THIS IN THE GRAPH BELOW

Example on Doing an Inverse of a Function:

1. ƒ(x) = 2x + 4

y=2x + 4---Change the ƒ(x) to a y.

x=2y + 4---Change the original y to an x and change the original x to a y.
-4        -4---Subtract 4 from both sides.

x - 4= 2y
  2       2---Divide by 2 from both sides.

y= x - 4
        2

ƒ⁻¹(x)= x - 4
                2---Change the y back to ƒ⁻¹(x). 

The transformation of graphs

9/25/12

Every function is based off a parent function. These parent functions are then modified to create the new function. For instance:

 Use the function f(x) = x^2 + 3. The parent function for this is f(x) = x^2. As with the equation y = mx + b, the 3 here is the y intercept, or where the graph will begin at when x=0. The new graph should look something like this.

 

 

 

For horizontal movement, it works a little bit differently. If the number is placed with x in parenthesis, the number will affect where the graph starts on the x axis. A positive number shifts the graph to the left, and vice versa. An example is y = (x – 1)^2.

 

 

Graphs can also be reflected. The graph of y = x^2 may look like this:

We can reflect this graph by adding a negative sign in front of the x. this would look like y = - x^2, or:

 

 

Finally, graphs can become wider or narrower. Take the parent function of f(x)=IxI.

The initial function looks like:

 

 

 

By multiplying the absolute value of x by two, the graph becomes much narrower because the y increases much more rapidly, so f(x)=2IxI looks like:

 

 

 

 

Arithmetic Combinations of Functions

Two functions can be combined to make new functions, this is called arithmetic combinations of functions. Say you have two equations...

 f (x) = 3x - 7   and   g (x) = x + 5

f (x) and g (x) both represent the y values of two different functions so these can be combined to make new functions both algebraicly and graphically

Algebraic soultion
    
     Sum:   (f + g) (x) which equals f (x) + g (x) ... so...= (3x -7) + (x + 5)
                                                                                 = 4x - 2

     Difference: (f + g) (x) which equals f (x) - g (x) ... so... = (3x-7) - (x+5)
                                                                                        = 2x - 12

     Product: (fg) (x) which equals f (x) * g (x) ... so... = ( 3x-7) (x+5)

                                   =

                                                                               
   Quotient: (f/g) (x) which equals f (x) / g (x) ... so... = (3x-7) / (x+5)
                                                                               x can't equal -5

Graphic Solution

     Very much the same as solving algebraicly. For the sum, you add the y points of each function and you get your new point. For the difference you subtratc. For product you multiply. For Quotient you divide.


                              Co-Published by Jack LaFave

Questions/muddy points through Section 1.4

Please comment on this post using the link below.

Write a question or concern you currently have regarding any of the material we've covered so far in Chapter 1. 

Function Notation

Function Notation (Section 1.1)

Definition: a "name" or "label" given to a specific equation so that it can be easily referenced

Why Function Notation? Function Notation provides you with more flexibility in your equation; you can use more than one function at a time without mixing up equations, and also, it is usefully explanatory.

• F = name of the function 
• F(x) = output value at input value of x
• Input = independent variable 
• Output = dependent variable

F(x) is the value of "f" at "x" or "f" of "x".

F(x) is the same as the y coordinate.

Example

1. Evaluate f(x) = 3 - 2x when f(-1) and f(0).

Step 1: plug in -1 for every x variable

• f(-1)= 3 - 2(-1) 

Step 2: Solve

• f(-1) = 3 - 2(-1) 
• f(-1) = 5

Hint: Other names can be given to equations such as: g(x) or q(t) 

Example

2. What does the function notation g(8) represent? 

Answer: the output of the function "g" when the input is "8" 

Evaluating a Difference Quotient

How to Answer

The goal in evaluating a difference quotient is to simplify, not solve for a variable.

This is the basic difference quotient:

Let's start with a simple function:

Now you substitute each f(blank) by plugging it into the function and substituting for x. Think of it as f(2). Plug that into the function and it becomes 2(2)=4. It is the same thing for f(x+h). Plug it in and it becomes 2(x+h)=2x+2h. So now let's evaluate the difference quotient.

Evaluate:,

First step it to plug in

 Now Distribute:Then combine like-terms:

 Simplify and divide out h

And your answer is 2 and

That's all there is to it. But lets look at one more problem.

Knowing When to Stop

Once again, the goal in evaluating a difference quotient is to simplify, not solve for a variable. Let's take the same problem, different function.

First Substitute:

 Use FOIL:  Simplify:

 Factor out h: Simplify

 And this is the answer:, 

DONE! Thats it. Don't do anything else. Don't set it equal to zero and try and solve for x and h.

Alright, I hope this helps. Feel free to ask questions if you have any. Thank you!