Wednesday, October 31, 2012
Fundamental Identities
Tuesday, October 30, 2012
The Unit Circle
The Unit Circle
What is the Unit Circle?
The unit circle is a circle whose center is at the origin with a radius of one. Because the radius is 1, you can directly measure sine and cosine. If a point on the circle is on the terminal side of an angle in standard position, then the sine of such an angle is the y-coordinate of the point, and the cosine of the angle is the x-coordinate of the point.

The Pythagorean Theorem states that
for a right angled triangle, the square of the long side equals the sum of the
squares of the other two sides:
x2+ y2 = 12
But 12 is just 1, so:
x2+ y2 = 1
(the equation of the unit circle)
(the equation of the unit circle)
Using Coordinates to Find Trigonometric Functions
The coordinates x and y are two functions of the real variable theta. You can use the coordinates to define the six trigonometric functions of theta.
The point of the unit circle is to make math easier and neater. For example, in the unit circle, you have, for any angle theta, the trig values for sine and cosine are sin(θ) = yand cos(θ) = x. Working from this, you can take the fact that the tangent is defined as being tan(θ) = y/x, and then substitute for x and y to easily prove that the value of tan(θ)also must be equal to the ratio sin(θ)/cos(θ).

Special Points of Interest on the Unit Circle
It is very important to memorize the sine and cosine of the angles created by special right triangles for future use.
Here is a video on how to easily remember the Unit Circle-
For further help, please watch these videos-
http://www.youtube.com/watch?v=ZffZvSH285c
http://www.youtube.com/watch?v=DIGoK51u0KQ
http://www.youtube.com/watch?v=3GgO7Q_kg8Q
-Kenji Johnston
Monday, October 22, 2012
Questions/Muddy points for Chapter 2
Please comment on this post using the link below.
Write a question or concern you currently have regarding any of the material we've covered so far.
Write a question or concern you currently have regarding any of the material we've covered so far.
Thursday, October 18, 2012
Rational Functions
For graphing rational functions we need to follow these
steps:
1) Find any intercepts, if there are any. (Remember to find the y-intercept with f(0)
and x intercepts by setting the numerator equal to zero).
2) Find the vertical asymptotes by setting the
denominator equal to zero and solving.
3) Find the horizontal asymptote.
4) The vertical asymptotes will divide the number
line into regions. In each region graph at least one point in each
region. This point will tell us whether the graph will be above or below
the horizontal asymptote and if we need to we should get several points to
determine the general shape of the graph.
5) Sketch the graph.
Example:
Sketch the graph of the following function.

This time notice that if we were to plug in 



Now, let’s see if we’ve got x-intercepts.
So, we’ve got two of them.
We’ve got one vertical asymptote, but there may be more so let’s go through the process and see.
So, we’ve got two again and the three regions that we’ve got are 











Next, the largest exponent in both the numerator and denominator is 2 so by the fact there will be a horizontal asymptote at the line,
Now, one of the x-intercepts is in the far left region so we don’t need any points there. The other x-intercept is in the middle region. So, we’ll need a point in the far right region and as noted in the previous example we will want to get a couple more points in the middle region to completely determine its behavior.



Here is the sketch for this function.

Tuesday, October 16, 2012
1. The line x = a is a vertical asymptote of the graph of f if 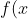 \to)
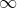 or
or
2. The line y = b is a horizontal asymptote of the graph of f if 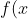 \to \ b) as
as
The line x = 0 is a vertical asymptote of the graph of f, shown below.
The graph of f also has a horizontal asymptote - the line y = 0. This means the values of f(x) = 1/x approach zero as x increases or decreases without bound.
decreases without bound. increases without bound.
Asymptotes of a Rational Function
Let f be the rational function
where N(x) and D(x) have no common factors.
1. The graph of f has vertical asymptotes at the zeros of D(x).
2. The graph of f has at most one horizontal asymptote determined by comparing the degrees
of N(x) and D(x).
a. If n > m, the line y = 0 (the x-axis) is a horizontal asymptote.
b. If n = m, the line y =  is a horizontal asymptote.
is a horizontal asymptote.
c. If n > m, the graph of f has no horizontal asymptote.
;ljk
Subscribe to:
Comments (Atom)



